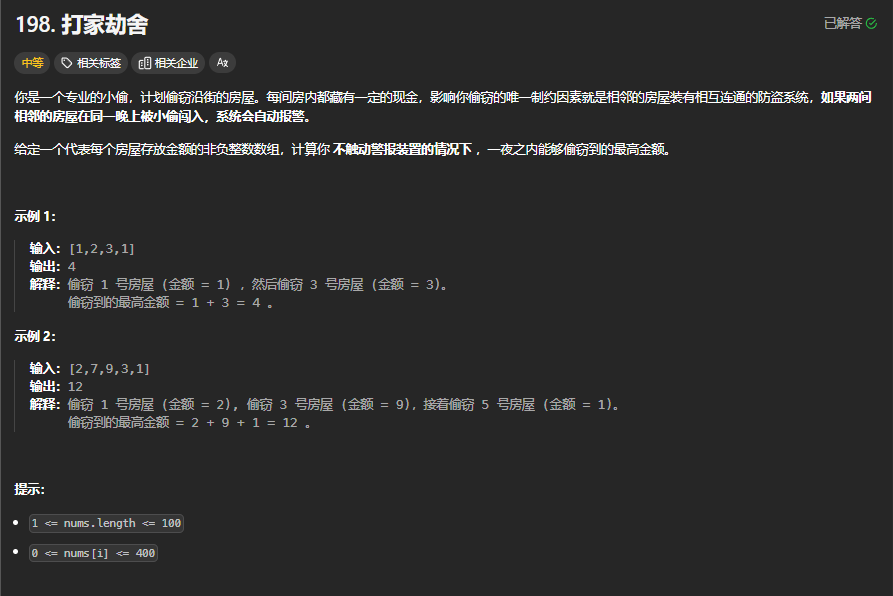
题目
解题思路
这是一个典型的动态规划问题。对于每个房屋，我们有两种选择：
- 偷这个房子：那么就不能偷相邻的前一个房子，但可以偷前前一个房子
- 不偷这个房子：那么最大金额就是偷到前一个房子为止的最大金额
定义状态：
状态转移方程：
- dp[i] = max(dp[i-1], dp[i-2] + nums[i])
- dp[i-1]：不偷第i个房子
- dp[i-2] + nums[i]：偷第i个房子，加上前前个房子的最大金额
边界条件：
- dp[0] = nums[0]：只有一个房子时
- dp[1] = max(nums[0], nums[1])：有两个房子时，选择金额较大的那个
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution:
def rob(self, nums: List[int]) -> int:
if not nums:
return 0
if len(nums) == 1:
return nums[0]
dp = [0] * len(nums)
dp[0] = nums[0]
dp[1] = max(nums[0], nums[1])
for i in range(2, len(nums)):
dp[i] = max(dp[i-1], dp[i-2] + nums[i])
return dp[-1]
|
复杂度分析
- 时间复杂度：O(n)，其中n是数组的长度。我们只需要遍历一次数组。
- 空间复杂度：O(n)，需要一个dp数组来存储状态。
优化空间复杂度
注意到我们每次状态转移只需要前两个状态，因此可以只用两个变量来维护状态，将空间复杂度优化到O(1)：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution:
def rob(self, nums: List[int]) -> int:
if not nums:
return 0
if len(nums) == 1:
return nums[0]
prev2, prev1 = nums[0], max(nums[0], nums[1])
for i in range(2, len(nums)):
current = max(prev1, prev2 + nums[i])
prev2, prev1 = prev1, current
return prev1
|
总结
以下是我自己的实现的方法。发现max函数 时间消耗比我的大，所以用大小判断时间更短。但是我在想这个到题的时候，是没有想出那个这个公式。dp[i] = max(dp[i-1], dp[i-2] + nums[i])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution:
def rob(self, nums: List[int]) -> int:
l = len(nums)
if l==0:
return 0
if l==1:
return nums[0]
dp = [0]*l
dp[0]= nums[0]
dp[1]= nums[1]
pre2_maxvalue = dp[0]
for i in range(2,l):
if dp[i-2]>pre2_maxvalue:
pre2_maxvalue = dp[i-2]
print(f'{pre2_maxvalue=}')
dp[i] = pre2_maxvalue+nums[i]
print(f'{i=}')
print(f'{dp[i]=}')
return max(max(dp[l-3],dp[l-1]),max(dp[l-2],dp[l-4]))
|
